排序算法-简单排序

冒泡排序

冒泡排序（Bubble Sort），是一种计算机科学领域的较简单的排序算法。

这个算法大家应该很熟悉了，下面进入正题

原数组{4,5,6,3,2,1} 要求升序排列

冒泡排序原理

比较相邻的元素。如果前一个元素比后一个元素大，就交换这两个元素的位置。
对每一对相邻元素做同样的工作，从开始第一对元素到结尾的最后一对元素。最终最后位置的元素就是最大值。

冒泡排序Api设计

类名	Bubble
构造方法	Bubble()：创建Bubble对象
成员方法	1.public static void sort(Comparable[] a)：对数组内的元素进行排序 2.private static boolean greater(Comparable v,Comparable w):判断v是否大于w 3.private static void exch(Comparable[] a,int i,int j)：交换a数组中，索引i和索引j处的值

冒泡排序的代码实现

package com.bestrookie.sort;

/**
 * @author : bestrookie
 * @date : 20:30 2021/5/9
 */
public class Bubble {
    public static void sort(Comparable[] a){
        for (int i = 0; i < a.length-1; i++) {
            for (int j = 0; j < a.length-1; j++) {
                if (greater(a[j],a[j+1])){
                    exch(a,j,j+1);
                }

            }
        }
    }
    /**
     * 判断元素v是否大于元素w
     * @param v 做比较的数据
     * @param w 作比较的数据
     * @return 是否相等
     */
    public static boolean greater(Comparable v,Comparable w){
        return v.compareTo(w) > 0;
    }

    /**
     * 交换位置
     * @param a 原来的一组数据
     * @param i 位置
     * @param j 位置
     */
    public static void exch(Comparable[] a,int i ,int j){
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

冒泡排序时间复杂度分析

冒泡排序使用了双层for循环，其中内层循环的循环体是真正完成排序的代码，所以，我们分析冒泡排序的时间复杂度，主要分析一下内层循环体的执行次数即可。

在最坏情况下，也就是假如要排序的元素为{6,5,4,3,2,1}逆序，那么：

元素比较的次数为：

(N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2; *

元素交换的次数为： (N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2;

总执行次数为： (N^2/2-N/2)+(N^2/2-N/2)=N^2-N;

按照大O推导法则，保留函数中的最高阶项那么最终冒泡排序的时间复杂度为O(N^2).

选择排序

选择排序相比较冒泡排序而言更加简单直观

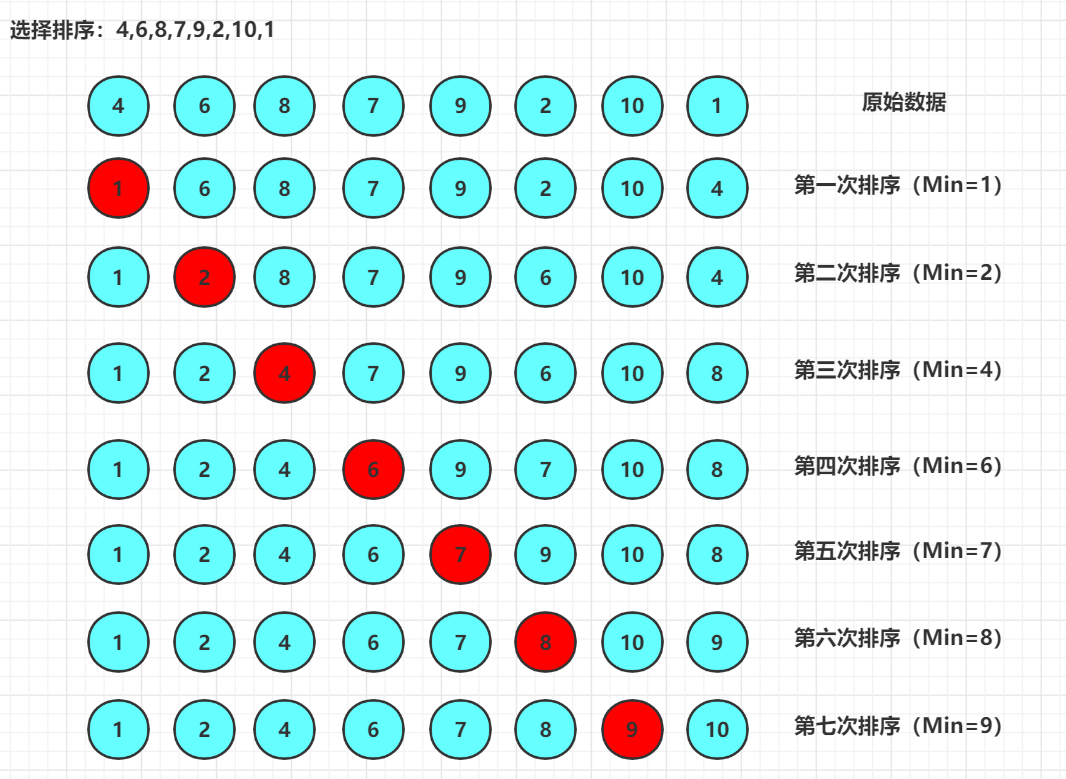
需求：排序前：{4,6,8,7,9,2,10,1} 排序后：{1,2,4,5,7,8,9,10}

选择排序原理

每一次遍历的过程中，都假定第一个索引处的元素是最小值，和其他索引处的值依次进行比较，如果当前索引处的值大于其他某个索引处的值，则假定其他某个索引出的值为最小值，最后可以找到最小值所在的索引
交换第一个索引处和最小值所在的索引处的值

选择排序Api设计

类名	Selection
构造方法	Selection()：创建Selection对象
成员方法	1.public static void sort(Comparable[] a)：对数组内的元素进行排序 2.private static boolean greater(Comparable v,Comparable w):判断v是否大于w 3.private static void swap(Comparable[] a,int i,int j)：交换a数组中，索引i和索引j处的值

选择排序的代码实现

package com.bestrookie.sort;
/**
 * @author : bestrookie
 * @date : 21:38 2021/5/9
 */
public class Selection {
    public static void sort(Comparable[] a){
        for (int i = 0; i < a.length-1; i++) {
            int minIndex = i;
            for (int j = i+1; j < a.length ; j++) {
                if (generate(a[minIndex],a[j])){
                    minIndex = j;
                }
            }
            swap(a,i,minIndex);
        }
    }
    /**
     * 比较元素v是否大于元素w
     * @param v 元素v
     * @param w 元素w
     * @return 是否大于
     */
    public static boolean generate(Comparable v, Comparable w){
        return v.compareTo(w) > 0;
    }

    /**
     * 交换i,j的位置
     * @param a 原数组
     * @param i 交换的位置
     * @param j 交换的位置
     */
    public static void swap(Comparable[] a,int i,int j){
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;

    }
}

选择排序的时间复杂度分析

选择排序使用了双层for循环，其中外层循环完成了数据交换，内层循环完成了数据比较，所以我们分别统计数据交换次数和数据比较次数：

数据比较次数：

(N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2;

数据交换次数：

N-1

时间复杂度：N^2/2-N/2+（N-1）=N^2/2+N/2-1;

插入排序

插入排序（Insertion sort）是一种简单直观且稳定的排序算法。插入排序的工作方式非常像人们排序一手扑克牌一样。开始时，我们的左手为空并且桌子上的牌面朝下。然后，我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置，我们从右到左将它与已在手中的每张牌进行比较，如下图所示：

来个小需求：

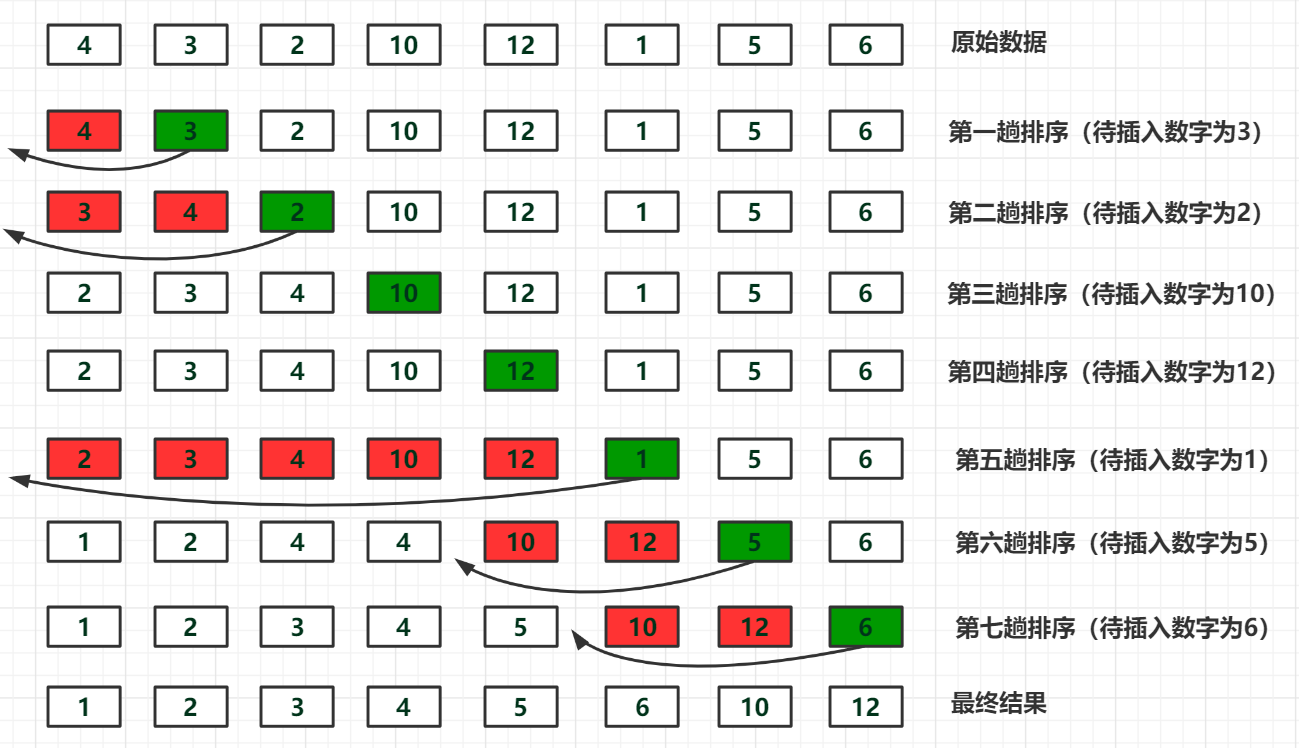
排序前：{4,3,2,10,12,1,5,6}

排序后：{1,2,3,4,5,6,10,12}

插入排序原理

1.把所有的元素分为两组，已经排序的和未排序的；

2.找到未排序的组中的第一个元素，向已经排序的组中进行插入；

3.倒叙遍历已经排序的元素，依次和待插入的元素进行比较，直到找到一个元素小于等于待插入元素，那么就把待插入元素放到这个位置，其他的元素向后移动一位；

插入排序Api设计

类名	Insertion
构造方法	Insertion()：创建Insertion对象
成员方法	1.public static void sort(Comparable[] a)：对数组内的元素进行排序 2.private static boolean greater(Comparable v,Comparable w):判断v是否大于w 3.private static void swap(Comparable[] a,int i,int j)：交换a数组中，索引i和索引j处的值

插入排序代码实现

package com.bestrookie.sort;

/** 插入排序
 * @author : bestrookie
 * @date : 21:49 2021/5/10
 */
public class Insertion {
    public static void sort(Comparable[] a){
        for (int i = 1; i < a.length ; i++) {
            for (int j = i; j > 0 ; j--) {
                if (greater(a[j-1],a[j])){
                    swap(a,j-1,j);
                }else {
                    break;
                }
            }
        }
    }
    public static boolean greater(Comparable v,Comparable w){
        return v.compareTo(w) >0;
    }
    public static void swap(Comparable[] a,int i,int j){
        Comparable temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}